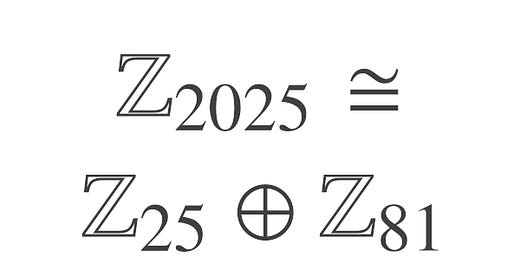Two concrete posts on group theory
Many of you reading this are new to this newsletter. If you came for the mathematical posts, you’ll enjoy this one. If you came for posts with less math, hang in there. I don’t know what I’ll write about next, but I try to not write many posts in a row on the same topic.
There’s a tradition in mathematical writing to use the current year as a number in an example problem. Usually this implies that the number is not special, that you could in principle pick any number, so why not pick the year.
This morning I wrote a post on finding all Abelian (commutative) groups with 2025 elements. Using n = 2025 makes the post concrete. I start there, and then by the end of the post give the general solution for any n.
Incidentally, if you want to find all groups of order 2025, not just the Abelian ones, that’s much more complicated. There are a total of 63 groups of order 2025, but the non-Abelian groups are not nearly as easy to enumerate.
It’s possible to list the Abelian groups of order 2025 in a way that looks entirely different from the list given in the post discussed above. The two lists consist of the same groups, “same” in the sense that the corresponding groups from the two lists are isomorphic.
I use this example to discuss when it is and when it isn’t important to be explict about what you mean for two objects to be the same. When we say there are 10 Abelian groups of order 2025, we mean that there are 10 groups up to isomorphism.